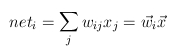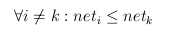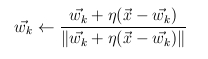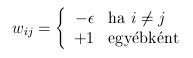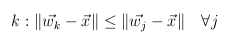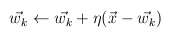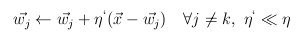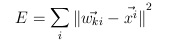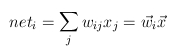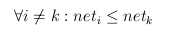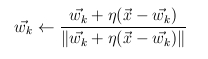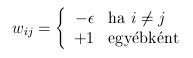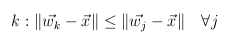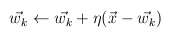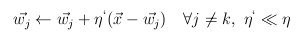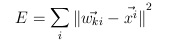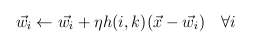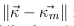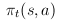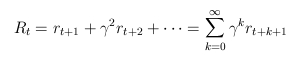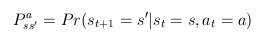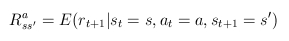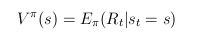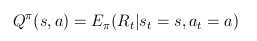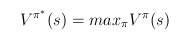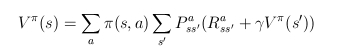Mobil robotok szimulációja speci 6. óra

Önszervezõdés

tanulás más formája
példák mindenféle tanítás nélkül
a bemenet belsõ struktúráját kell felfedezni
osztályozás, kluszterezés, dimenziószám-csökkentés, tulajdonság-kiemelés
csillagászat, képi megjelenítés

Csoportosítás

mindennapi élet gyakori feladata
csoportokba rendezése, csoportokon belül nagy hasonlóság, a csoportok között kis hasonlóság
hierarchikus klaszter analízis: osztályok folytonos összevonása
k-várható érték módszere: Gauss eloszlások paramétereinek becslése
teljes összekötöttségû, kétrétegû háló
a bemeneti réteg az adatok dimenziója, a kimeneti réteg a csoportok száma
hálósúlyok módosítása
kezdeti véletlen súlyok
hálódinamika
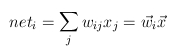
egységvektorok
maximum
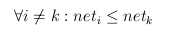
a kimenet: a legnagyobb 1, a többi 0 (versenyzés)
tanulás során egyedül a gyõztes neuron súlyai változnak
súlyvektor elforgatása a példa irányába
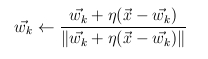
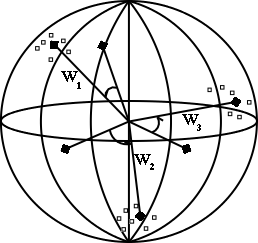
csoportosítás:súlyvektorok a térnek azon részei felé fordulnak el, ahol sok a példavektor
súlyvektor, mint osztálycímke
maximumkeresés nem lokális feladat, neurális hálóval másképp kell megoldani
MAXNET
teljes összekötöttség, fix súlyokkal
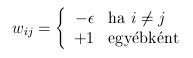
minden neuron kimenete 0-hoz konvergál, kivéve a legnagyobbé
normalizálás nélkül: egy a példával kis szöget bezáró, de hosszú súlyvektor példával való szorzata nagyobb lenne, mint egy kis abszolút értékû, de közeli súlyvektoré
általánosabb megoldás
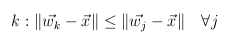
súlyok módosítása e szerint
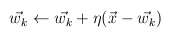
távolságfüggvény és bemenet választásának fontossága
mozdulatlan súlyvektorok elkerülése
sok neuron, magas dimenziószám: súlyvektor sohasem lesz gyõztes
súlyvektorok egyenletes inicializálása
szivárgásos tanulás
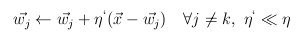
frekvencia-érzékeny tanulás
megállás kérdése, hibafüggvény szerepe

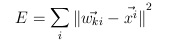
Kohonen-féle tulajdonságtérkép

winner-take-all <-> lágy versenyzés
Kohonen eredménye a nyolcvanas évekbõl
háló struktúrája megfelel a csoportosításnál látottaknak
gyõztes kiválasztása sem tér el
azonban van egy szomszédsági reláció
bármilyen kapcsolati forma: négyzetháló, lánc, kör,...
szomszédsági reláció != háló kapcsolatai
tanulás új szabálya
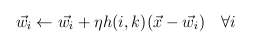
h gyõztes és az éppen vizsgált neuron közötti kapcsolat függvénye
h nagyjából tetszõleges, h(k,k) = 1
ha h mindenütt 0, akkor a csoportosításhoz jutunk vissza
négy, nyolc szomszédság síkban, hat, huszonhat szomszédság térben
Gauss függvény: jobb mozgás, kevesebb mozdulatlan neuron, de hátrány nagyobb számításigény
idõben csökkenõ szomszédság
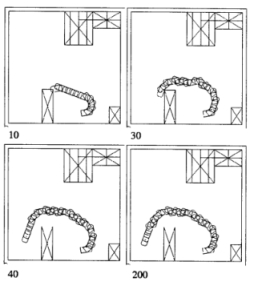
az idõ elõrehaladtával a háló mintegy kifeszíti a négyzet területét
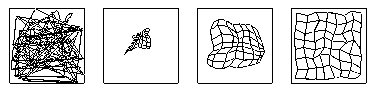
tér diszkrétizációja
láthatóvá teszi a példák terének struktúráját
navigáció

Önszervezõdési eljárások demonstrációja

Internetrõl letölthetõ programok, demok
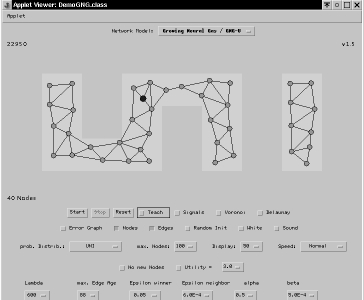
Loos és Fritzke DemoGNG programja
alaptípusok és újak is
neurális gáz: idõben csökkenõ szomszédság
növekvõ neurális gáz: egyre több neuron közelít

Önszervezõdés robotszimulációban

Nehmzow és Smithers, 1990 a Kohonen-féle önszervezõdõ tulajdonságtérkép egy robot navigációjához
külvilág belsõ reprezentációja
három fõ modul
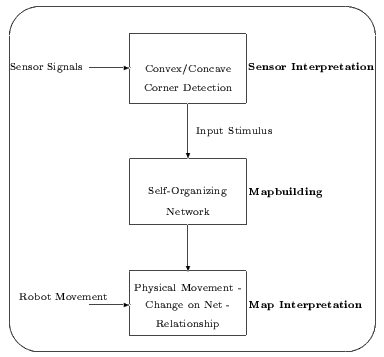
térkép bijekció a lehetséges állapotok terébõl a térkép terébe
nem csak felülnézeti térkép, hanem telefonkönyv vagy a családfa is lehet
hasonlít a csoportosításnál bemutatott elsõ változathoz (normálás)
50 neuronból álló hálózat, gyûrû
egydimenziós szomszédsági reláció
a gyõztes súlymódosulásában két-két szomszédja osztozhat
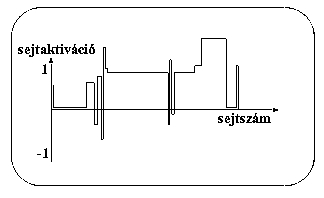
a kimenet nem lesz binárissá alakítva
helyek meghatározása nem a gyõztes neuronhoz rendelt pozíció alapján történik
50 neuron által alkotott összetett válasz egyedisége a pozíció címe
a cím egyediségéhez a példáknak megfelelõen kell reprezentálnia a külvilágot
elõször akadálykikerülés és véletlen mozgás
példák a szenzorok értékei és két akadállyal való találkozás közben megtett távolság
csukott szemmel sétálásból térkép
falkövetés
elsõ modul: sarok konvex vagy konkáv
példa: az aktuális és a megelõzõ sarok irányultsága és távolsága
az eljárás az ismert formában zajlik
robot a fal mellett több kört megtesz
sarkonként példa keletkezett
a kezdetben nagy eta minden lépésben 5 százaléknyit csökken
három kör után sarokkijelölés
ezután különbségnorma számítása minden sarokra
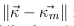
megfelelõ belsõ reprezentációt -> jelöltnél kisebb norma, mint máshol
H sarok felismerése
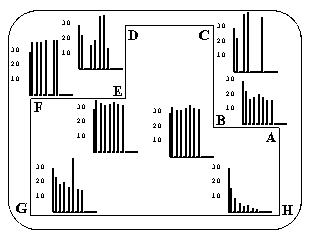
C és F, valamint B és E problémás
példák kibõvítése két sarokra nem elég (B és E)
még mindig kevés
példák kibõvítése három sarokra már elég (B és E)
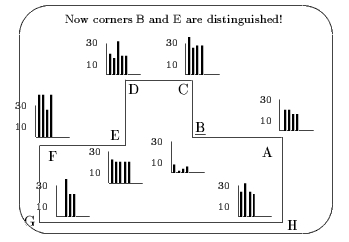
elõre meghatározott mozgás, de mûködõ térkép, robusztus viselkedés

Megerõsítéses tanulás

tanulás más formája
hétköznapjaink szerves része
járás, kockatorony építése, vezetés, bioreaktor
nincs tanító, a környezet reakcióiból következik a tevékenység jó vagy rossz eredménye
meghatározott környezet, cselekvések
diszkrét idõ
környezet cselekvésektõl megváltozik, új állapot
cselekvésért járó jutalom
megerõsítéses tanulás struktúrája
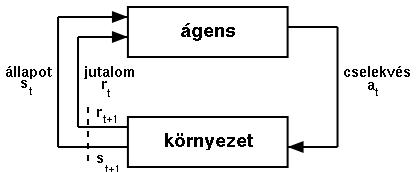
döntési függvény: adott állapotban, adott cselekvés végrehajtásának valószínûsége
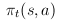
tanulás a döntési függvény módosításának folyamata
szemétgyûjtõ robot példája
döntés haladási irány, állapot: robot és szemét helye, akku
általában nincs jutalom, csak szemét felszedésekor, büntetés lemerült akkunál
nem szimplán a legnagyobb jutalom kiválasztása, hanem legnagyobb várható nyereség
véges és végtelen eset
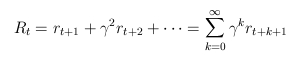
felfedezés, kiaknázás dilemmája (exploráció-exploitáció)

Kiértékelõ függvények

a döntési függvény (pi) közvetlen megadása általában nem lehetséges, a megoldáshoz további függvények bevezetése szükséges
Markov tulajdonság: nem kell korábbi állapotokhoz visszanyúlni a helyzet megismeréséhez (sakkállás)
és véges az állapotok és a cselekvések halmaza
akkor a teljes feladat-specifikáció az alábbi két egyenletrendszer
átmenet valószínûségek
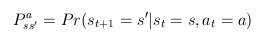
várható jutalom
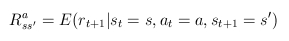
az egyenletek nincsenek mindig a tanuló birtokában, de megismerhetõek.
teljes feladat-specifikáció esetén sem könnyû a megoldás (sakk, Rubik-kocka)
állapotérték-függvény: mennyire értékes az adott állapot a feladat szempontjából, az aktuális pi szerint
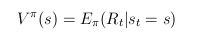
akcióérték-függvény:mennyire értékes az adott állapotban az adott cselekvés a feladat szempontjából, az aktuális pi szerint
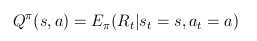
leggyakrabban ezeken és a döntési függvényen dolgozik a tanulás
tanulás: értékfüggvények közelítése -> döntési függvény számítása -> értékfüggvények növekedése -> ...
optimális döntési függvény: minden állapotban a legjobb cselekvést választja
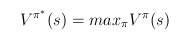
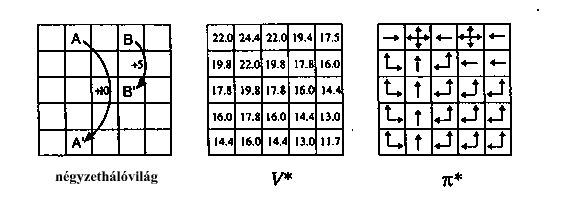
négyzetháló-világban optimális állapotérték-függvény és optimális döntési függvény

Megoldási módszerek

dinamikus programozás
- teljes feladat-specifikáció ismert
- értékfüggvény rekurzív kiszámítása Bellman-egyenlõség alapján
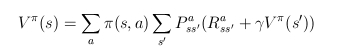
- döntési függvény mohó módosítása állapotérték-függvény szerint
- iteráció konvergenciáig
Monte-Carlo módszerek
- nem ismert feladat-specifikáció
- a tanuló epizódokat gyárt
- jutalmak átlaga az érintett állapotokra és cselekvésekre meghatározott akcióérték-függvény
- algoritmusa
idõbeli differenciák
- Monte-Carlo modellnélkülisége
- értékfüggvény rekurzív elõállítása, nem kell az epizódokat végigvárni
- konvergencia: korlátos jutalom, minden állapot-cselekvés páros tetszõlegesen sokszor legyen kiválasztva
- Q-tanulás
egyéb módszerek: megbízhatósági nyomok, függvényapproximáció neurális hálóval

Megerõsítéses tanulás Java nyelven

Navigáció megerõsítéses tanulása

megerõsítéses tanulás jól használható, ha idõ és a tér is diszkrét módon definiált
robotikában nem ez a helyzet: folytonos tér, végtelen sok állapot és cselekvés
térdiszkrétizáció önszervezõdéssel
B. Kröse és M. Eecen munkája: Kohonen-térképre épített dinamikus programozás
16 távolságszenzor + iránytû
térkép a szenzortérben van, mégis a valós világ pontjait reprezentálják
Kohonen szomszédság elemei nem feltétlenül fizikailag közvetlenül elérhetõ pontokat kötnek össze
a szomszédsági relációk helyett a dinamikus programozás hozza létre az állapotátmenetekhez szükséges cselekvések döntési függvényét
átmenetek valószínûségének meghatározása a robot szabadon közlekedésével
közvetlen jutalom: a távolság és a tárgyaknak való ütközések függvényében jön létre
teljesen specifikáltság -> dinamikus programozás
egy önszervezõdés során elõálló térkép
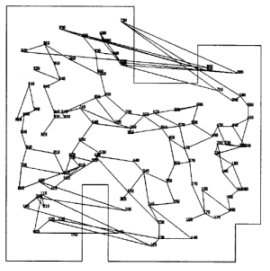
a robot navigációja